Principio de superposición
Es un hecho experimental que en muchas clases de ondas , dos o más de ellas pueden atravesar la misma zona del espacio independientemente una de la otra. Esto significa que la perturbación resultante es en instante determinado la suma de las perturbaciones individuales. Este proceso se denomina superposición, por ejemplo en el sonido, distinguimos las notas de los diversos instrumentos que están tocando en una orquesta. Este principio queda claramente expuesto en: http://www2.biglobe.ne.jp/~norimari/science/JavaEd/e-wave2.html
Interferencia entre dos ondas
Una característica muy importante del movimiento ondulatorio es el fenómeno de interferencia. Esto ocurre cuando dos o más ondas coinciden en el espacio y en el tiempo.
Consideremos dos fuentes S1 y S2 que oscilan en fase con la misma frecuencia angular y amplitudes A1 y A2. Sus ondas esféricas armónicas monocromáticas son: y1(t)
=
A1
sen
(wt
+
kr1)
y
y2(t) = A1 sen (wt + kr2)
donde
r1
y
r2
son
las
distancias
desde
cualquier
punto
a
S1
y
S2.
La
amplitud
de
las
ondas
en
P
no
tienen
la
misma
amplitud
ya
que
esta
disminuye
según
1/r.
Cuando comparamos las ondas con la ecuación del MVAS y = A sen (wt + a), las cantidades Kr1 y y Kr2 juegan el mismo papel que las fases iniciales.
Entonces el desfasaje entre los dos movimientos ondulatorios en cualquier punto P es:
d
=
Kr1
–
Kr2
=
2p/l
(r1
–
r2)
La amplitud resultante va a ser:
|
A = |
|
y
está
comprendida
entre
(y1
+
y2)
y
(y1
-
y2)
dependiendo
de
que
sea
cosd
=±1
Þ
d
=
2np
ó
(2n
+1)
p.
En
el
primer
caso
tenemos
máximo
refuerzo
de
los
movimientos
ondulatorios,
o
interferencia
constructiva,
y
en
el
segundo
hay
máxima
atenuación
o
interferencia
destructiva.
| í | 2np interferencia constructiva | í | 2np interferencia constructiva | ||
| d |
2p/l
(r1
–
r2) |
||||
| (2n +1) p interferencia destructiva | (2n +1) p interferencia destructiva |
| í |
nl
interferencia
constructiva |
|
| es decir : r1 – r2 = | ||
|
(2n
+1)
l/2
interferencia
destructiva |
Cuando r1 – r2 sea igual a ±l, ±2l, ±3l...los movimientos se refuerzan. Cuando r1 – r2 sea igual a ±1/2l, ±3/2l, ±5/2l...los movimientos se atenúan. Tendremos una sucesión de superficies nodales y ventrales. r1 – r2 = cte define una hipérbola cuyos focos son S1 y S2
Las superficies nodales se ven en http://members.nbci.com/surendranath/Interference/Ripint.html
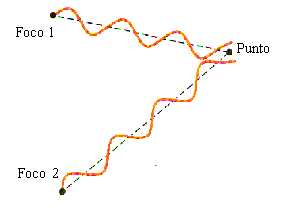
En cada punto del espacio, el movimiento ondulatorio tiene una amplitud distinta dada por:
|
A = |
|
La
razón
es
que
las
dos
fuentes
oscilan
con
la
misma
frecuencia
y
mantienen
un
desfasaje
constante,
y
se
dicen
que
son
coherentes.
Si
las
fuentes
no
son
de
la
misma
frecuencia,
o
si
sus
desfasajes
cambian
en
el
tiempo,
no
se
observa
diagrama
de
interferencia.
Esto
es
lo
que
ocurre
con
fuentes
ordinarias
de
luz.
En el siguiente applet mostramos la suma de dos ondas en las que podemos modificar la diferencia de fase, entre otras cosas. Suma las ondas en fase y en oposición de fase.
Sumamos las ondas en: http://www.vislab.usyd.edu.au/photonics/fibres/fizzz/sine/index.html
En 1801 el inglés T. Young dio un gran impulso a la teoría ondulatoria explicando el fenómeno de las interferencias y midiendo las longitudes de onda correspondientes a los distintos colores del espectro.
La teoría corpuscular era inadecuada para explicar el hecho de que dos rayos luminosos, al incidir en un punto pudieran originar oscuridad.Esto se comprueba en: http://vsg.quasihome.com/interfer.htm
