Movimiento en un campo magnético

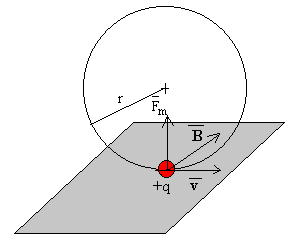
Una partícula que se mueve en un campo magnético experimenta una fuerza dada por el producto vectorial F_m=q·vxB. El resultado de un producto vectorial es un vector de

• módulo igual al producto de los módulos por el seno del ángulo comprendido qvB senq

• dirección perpendicular al plano formado por los vectores velocidad v y campo B.

• y el sentido se obtiene por la denominada regla del sacacorchos. Si la carga es positiva el sentido es el del producto vectorial vxB, como en la figura izquierda

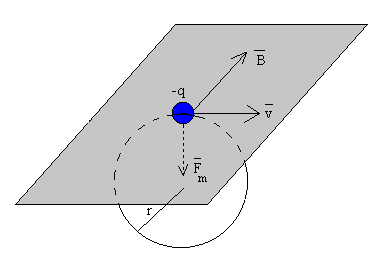
Si la carga es negativa el sentido de la fuerza es contrario al del producto vectorial vxB

Elementos a destacar de esta fórmula es que la fuerza magnética se deja notar, por tanto, sólo sobre partículas cargadas; para partículas neutras () se tendrá que . Un hecho aún más reseñable es que sólo actúa sobre partículas en movimiento. Si una partícula está en reposo respecto a nuestro sistema de referencia la fuerza magnética ejercida sobre ella, aunque esté cargada y exista un campo magnético, es nula.

La unidad de campo magnético en el Sistema Internacional es el Tesla.  Dimensionalmente un Tesla será Newton segundo entre metro Culombio.

• La fuerza magnética siempre es perpendicular a la trayectoria de la partícula. Por tanto el trabajo efectuado por la fuerza magnética es siempre cero y la energía cinética se conserva.

• Si, además de un campo magnético existiera un campo eléctrico podemos incluir esta fuerza en la Ley de Lorentz y, como la fuerza eléctrica es simplemente y podemos usar el principio de superposición

  

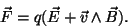
  En la siguiente página: http://surendranath.tripod.com/MovChgEleMag/MovChgEleMagApplet.html :

  Actividad: Un electrón penetra por la izquierda con velocidad v paralela al plano del papel donde escribes (v=10 m/s). En la zona del espacio delimitada por tu papel hay un campo magnético B (B = 1 T) uniforme, perpendicular al plano del papel y dirigido hacia arriba. Dibuja la trayectoria que sigue el electrón.

• Calcula el campo eléctrico que habría que aplicar para que los electrones mantuvieran rectilínea su trayectoria. Dibújalo.

Partícula sometida a un campo magnético constante y uniforme

Supongamos que tenemos una carga que entra en un campo magnético con una cierta velocidad y de tal forma que el campo magnético sea perpendicular a dicha velocidad. ¿Cómo se moverá en el seno de este campo?. Se puede entender de forma intuitiva que al se ejercerá una fuerza sobre la carga que, debe ser perpendicular a la velocidad con la que se desplaza la carga, y por tanto tendrá una componente exclusivamente normal a la trayectoria. Como en todo momento la fuerza es perpendicular a la trayectoria, porque así lo exige la ley de Lorentz, tendremos que la carga describirá una circunferencia, ya que estará sometida a una fuerza que creará una aceleración normal constante y una aceleración tangencial nula. Podemos por tanto igualar la fuerza centrípeta de este movimiento con la fuerza magnética y tener así que, si tomamos los módulos,

de donde se puede deducir que el radio de la trayectoria será

Una partícula cargada describe órbita circular en un campo magnético uniforme y perpendicular a la dirección de su velocidad. El radio de dicha órbita, puede obtenerse a partir de la aplicación de la ecuación de la dinámica del movimiento circular uniforme: fuerza igual a masa por aceleración normal.

Fuerza sobre un conductor rectilíneo.

En un elemento de longitud dl la fuerza será:

Si el conductor es rectilíneo F = i u_t x B L

http://www.walter-fendt.de/ph11s/lorentzforce_s.htm