
El físico Jean Biot dedujo en 1820 una ecuación que permite calcular el campo magnético B creado por un circuito de forma cualesquiera recorrido por una corriente de intensidad i.
![]()
B es el vector campo magnético existente en un punto P del espacio, ut es un vector unitario cuya dirección es tangente al circuito y que nos indica el sentido de la corriente en la posición donde se encuentra el elemento dl. ur es un vector unitario que señala la posición del punto P respecto del elemento de corriente, m0/4pi = 10-7 en el Sistema Internacional de Unidades.
Utilizamos la ley de Biot para calcular el campo magnético B producido por un conductor rectilíneo indefinido por el que circula una corriente de intensidad i.
El campo magnético B producido por el hilo rectilíneo en el punto P tiene una dirección que es perpendicular al plano formado por la corriente rectilínea y el punto P, y sentido el que resulta de la aplicación de la regla del sacacorchos al producto vectorial utx ur
Para calcular el módulo de dicho campo es necesario realizar una integración.
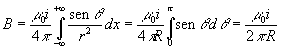
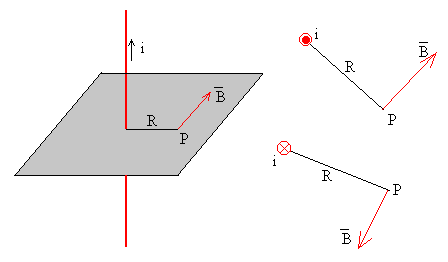
La dirección del campo magnético se dibuja perpendicular al plano determinado por la corriente rectilínea y el punto, y el sentido se determina por la regla del sacacorchos o la denominada de la mano derecha. En la siguiente página http://www.walter-fendt.de/ph11s/mfwire_s.htm viene muy esquemático.
4. Dos corrientes hacia afuera