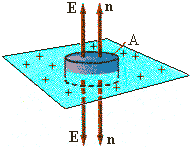

Campo eléctrico producido par una carga distribuida uniformemente sobre un plano

El plano tiene una carga s por unidad de área. De la simetría se deduce que las líneas son perpendiculares al plano. Tomando como superficie cerrada el cilindro de la figura, solo habrá flujo a través de las tapas del cilindro de área A. El flujo a través de una de esas tapas será EA. El flujo total será por tanto F=2EA. Por el teorema de Gauss sabemos que el flujo es:
Por tanto
|
|
=2EA |
siendo Q=s A Por consiguiente:
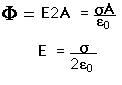
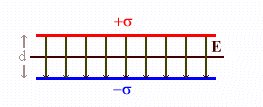
En la región fuera de los dos planos los campos son iguales y de sentido contrario y se anulan. En la región entre los planos los campos tienen el mismo sentido y el campo será el doble que para el caso de un solo plano
![]()
Campo creado por una línea indefinida cargada
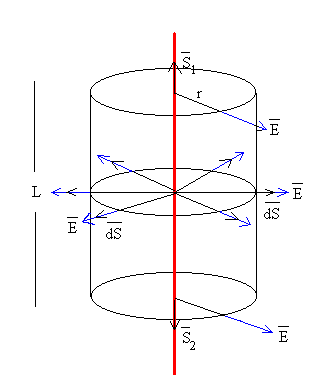 |
Para una línea indefinida cargada, la aplicación del teorema de Gauss requiere los siguientes pasos: |
1.-A partir de la simetría de la distribución de carga, determinar la dirección del campo eléctrico.
La dirección del campo es radial y perpendicular a la línea cargada
2.-Elegir una superficie cerrada apropiada para calcular el flujo
Tomamos como superficie cerrada, un cilindro de radio r y longitud L.
El cálculo del flujo, tiene dos componentes
- Flujo a través de las bases del cilindro: el campo E y el vector superficie S1 o S2 forman 90º, luego el flujo es cero.
- Flujo a través de la superficie lateral del cilindro: el campo E es paralelo al vector superficie dS. El campo eléctrico E es constante en todos los puntos de la superficie lateral, por lo que,
El flujo total es por tanto; E2p rL
3. Determinar la carga que hay en el interior de la superficie cerrada
La carga que hay en el interior de la superficie cerrada vale q=l L, donde l es la carga por unidad de longitud.
4.-Aplicar el teorema de Gauss y despejar el módulo del campo eléctrico
![]()