El número pi

El número pi es la constante que relaciona el perímetro de una circunferencia con la amplitud de su diámetro Π = L/D. Este no es un número exacto sino que es de los llamados irracionales, tiene infinitas cifras decimales. Ya en la antigüedad, se insinuó que todos los círculos conservaban una estrecha dependencia entre el contorno y su radio pero tan sólo desde el siglo XVII la correlación se convirtió en un dígito y fue identificado con el nombre "Pi" (de periphereia, denominación que los griegos daban al perímetro de un círculo), A lo largo de la historia, a este ilustre guarismo se le han asignado diversas cantidades. En la Biblia aparece con el valor 3, en Babilonia 3 1/8; los egipcios le otorgaban 4(8/9)²; y en China 3,1724. Sin embargo fue en Grecia donde la correspondencia entre el radio y la longitud de una circunferencia comenzó a consolidarse como uno de los más insignes enigmas a resolver. Un coetáneo de Sócrates, Antiphon, inscribió en el círculo un cuadrado, luego un octógono e ideó multiplicar la cantidad de lados hasta el momento en que el polígono obtenido ajustara casi con el anillo. Euclides precisa en sus Elementos, los pasos al límite necesarios y investiga un sistema consistente en doblar, al igual que Antiphon, el número de lados de los polígonos regulares y en demostrar la convergencia del procedimiento.
Arquímedes reúne y amplía estos resultados. Prueba que el área de un círculo es el la mitad del producto de su radio por la circunferencia y que la relación del perímetro al diámetro está comprendida entre 3,14084 y 3,14285.
En el siglo XVIII Georges Louis Leclerc, Conde de Buffon, naturalista francés, ideó un ingenioso método. llamado "La aguja de Buffon" que relaciona el número pi con el lanzamiento de una aguja sobre una superficie rayada.
Buffon demostró que si lanzamos, al azar, una aguja de longitud L sobre una superficie en la que hay dibujadas líneas paralelas separadas una distancia D (se puede repetir el cálculo utilizando un suelo de baldosas y una aguja), la probabilidad de que la aguja corte a una línea es:

Conforme se han desarrollado las matemáticas, en sus diversas ramas, álgebra, cálculo, etc, se han ido construyendo distintos artificios que permiten afinar cada vez más su valor. Uno de los casos más curiosos de la historia fue el del matemático inglés William Shanks, quien luego de un trabajo que le demandó casi veinte años, obtuvo 707 decimales en 1853. Desgraciadamente, Shanks incurrió en un error en el 528º decimal, y a partir de éste están todos mal.

Existen vías alternativas para calcular Π. Por ejemplo, podemos utilizar el periodo de un péndulo para realizar una estimación o usar procedimientos estadísticos. El sistema que se propone es parecido al del conde de Buffon, basado en la probabilidad.

Supongamos una circunferencia de radio 1, inscrito en un cuadrado Si creamos aleatoriamente pares de números (x,y) comprendidos entre cero y uno, si 1 ³ x² + y²el punto generado por x e y estará dentro del círculo mientras que si x² + y² ³ 1 los puntos estarán lógicamente en el cuadrado pero fuera del redondel. La probabilidad de que los puntos se hallen dentro de la circunferencia estará dada por la relación entre el área del círculo Π1² y la superficie del cuadrado (2²). Con una serie significativa de repeticiones la proporción entre los que caen en el círculo y fuera de él tiende a Π/4, y así obtenemos el valor de Π de una forma estadística.

Se ha creado un programa que genera al azar los pares de dígitos. Concretamente crea 10 millones de puntos y determina el número Π cada millón de tiradas. Al ser una operación estadística, a veces nos acercamos al valor correcto (conocido con miles de cifras) y otras nos alejamos. Con esta técnica determinamos 3 decimales correctos obteniendo un error cercano al 0.02%.

El número pi tiene infinitos decimales. Ha sido y es una ardua empresa calcularlos. Una labor quizá tan bella como inútil. Tan superfluo como coronar el Everest o atravesar el Atlántico en una chalupa, pero esencial en la naturaleza del hombre.

Código fuente cálculo de pi

// programa de pi, jesus ruiz felipe
import java.util.Random;

public class pi {
public static void main (String[] args) {

Random rnd = new Random();
double[] porcent = new double[12];
int b=0;
double x;
double y;
double a;
double n;
double valor;
valor=0;
a=0;
n= Math.pow(10.0, 9) ;
final double PI = 3.14159265358979323846;

System.out.println("Calculo de pi estadisticamente");
System.out.println("");

double j=0;
for (double i = 0; i < n; i++) {

x = (double)(rnd.nextDouble() );
y = (double)(rnd.nextDouble() );

if (x*x+y*y<=1){
a++;}
if ((i==n/1000)||(i==n/500)||(i==n/100)||(i==n/10)||(i==2*n/10)||(i==3*n/10)||(i==4*n/10)||(i==5*n/10)
||(i==6*n/10)||(i==7*n/10)||(i==8*n/10)||(i==9*n/10)){

j=4*a/i;
//j es pi

System.out.print(i+": pi es aprox. " + (double)Math.round(j*10000000)/10000000);
System.out.print("; pi es un " + (double)Math.round((100/PI)*j*10000000)/10000000);
System.out.print("% de PI. ");

double aux=valor-Math.abs(100-(100/PI)*j*1000/1000);

if ((double)Math.round(aux*1000)/1000<0){

System.out.println("Empeora "+ (double)Math.round(aux*1000)/1000);

valor= Math.abs(100-(100/PI)*j*1000/1000);
}
if ((double)Math.round(aux*1000)/1000>=0){

System.out.println("Mejora " + (double)Math.round(aux*1000)/1000);

valor= Math.abs(100-(100/PI)*j*1000/1000);
}}
}

System.out.println("");
System.out.println("El programa se ha corrido 10 millones de veces");

System.out.println("Estadisticamente pi es: "+4*a/n);
System.out.print( "Tiene un error del " + (100 - 400*a/(PI*n))+"%");
System.out.println("");
System.out.println("");
System.out.println("Revista Digital sociedadelainformacion.com");
System.out.println("Jesus Ruiz Felipe");

try {

System.in.read();
}catch (Exception e) {}
}
}

//lenguaje java

Solución aguja Buffon

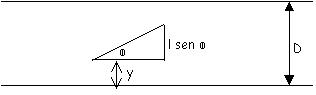
0< y < D

0 < F < P

La aguja cortará si: y + l senF ³ D Þ y ³ D - l senF

Área =

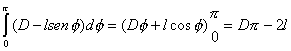Probabilidad de que no corte =

Probabilidad de que corte =