SIMULACIONES EN LA DIDÁCTICA DE LA FÍSICA
JESÚS RUIZ FELIPE. Profesor de Física y Química
La Física trata de esclarecer las fundamentos de los fenómenos naturales. Éstos
se describen matemáticamente mediante ecuaciones y expresiones que
interpretamos. Anticipamos sucesos, analizamos resultados, explicamos
situaciones naturales con principios y leyes que se plasman en unas sencillas
identidades matemáticas que esconden en su seno una ingente cantidad de
información. Los científicos, a lo largo de los siglos han ido inventando
conceptos que han ayudado mucho al entendimiento de la naturaleza. Magnitudes
que se conservan por ley o por principio, nos dan la clave de la comprensión,
temporal y mutable, de los fenómenos normales, siempre en una lenta aproximación
a la realidad. Como una sucesión convergente se van dando pequeños pasos hacia
un límite quizá inalcanzable. El profesor de Física expone a sus alumnos las
causas de los fenómenos naturales, mediante teorías que se han ingeniado en
las que se introducen esas magnitudes, donde hay establecidas unas relaciones
que se expresan en ecuaciones. El alumno ve “fórmulas”, aprende a
manejarlas con mayor o menor destreza, y en esa maña le va la nota. Con el
tiempo, y si continúa los estudios, empezará a relacionar situaciones, a
comprender explicaciones, a aprender.
Sin embargo la Física es muy rica en matices didácticos. Hay introducción de
conceptos, trabajo experimental, resolución de problemas, ideas previas, etc.
Si de lo que se trata es de hacer una descripción de la naturaleza se puede
intentar una narración no meramente matemática, sino detallar los fenómenos físicos
con modelos visuales. Idealizar los fenómenos mediante simulaciones permite
manipular y dirigir las magnitudes que intervienen, observando la contribución
de cada una de ellas de un modo perceptible. Sin olvidar el análisis matemático,
muchas simulaciones clarificarán fenómenos de tipo mecánico, ondulatorio, óptico,
etc. El estudio de formación de imágenes en dispositivos ópticos, las líneas
de fuerza, la reflexión, el efecto Doppler etc son ideales para una simulación
y control de variables.
El fenómeno explosivo de INTERNET, ha abierto unas expectativas insospechadas.
Las páginas web contienen texto, imágenes y applets o pequeños programas
interactivos escritos en lenguaje Java. La enseñanza de cualquier materia se
puede beneficiar de la extraordinaria facilidad de navegación, de la
posibilidad de tener a nuestra disposición inmediata la inmensa cantidad de
información de todo tipo almacenada en los miles de servidores repartidos a lo
largo y ancho del mundo, de la interactividad y el dinamismo que imprimen los
applets a las páginas web.
El estudiante puede interaccionar con un applet del mismo modo que lo hace con
cualquier otro programa Windows: introduce los valores iniciales, y controla la
evolución del sistema físico, observando los resultados en forma de texto, gráficos
y animaciones. Mediante el diálogo interactivo con el programa se pretende que
el alumno sea un partícipe activo en el proceso de aprendizaje, en vez de un
mero receptor de conocimiento.
Estos applets que circulan por la red, alojados en servidores remotos, hay que
adaptarlos a nuestro entorno educativo. Los profesores pueden elaborar sus
propios apuntes multimedia. No hace falta ser un diseñador ni un programador
para proporcionar a nuestros alumnos un material que permite estudiar la
asignatura de física desde otra perspectiva, menos convencional. No sólo
facilita al alumno el estudio individual sino que permite al docente mejorar sus
clases, sus exposiciones y sus explicaciones.
A corto plazo, los libros de texto incorporarán unidades didácticas en formato
multimedia o HTML. Es, sin duda, una apuesta ganadora de futuro.
Para ilustrar este artículo ofrecemos de muestra un botón. Cualquier profesor de Física sabe lo tedioso que resulta explicar el principio de Huygens y deducir a partir de éste los fenómenos de la reflexión y la refracción. Véase si este material no simplifica la labor:
Principio de Huygens
|
|
|---|
Alrededor de 1860 el físico danés Huygens propuso un mecanismo simple para trazar la propagación de ondas. Su construcción es aplicable a onda mecánicas en un medio material.
Un frente de onda es una superficie que pasa por todos los puntos del medio alcanzados por el movimiento ondulatorio en el mismo instante. La perturbación en todos esos puntos tiene la misma fase. Podemos trazar una serie de líneas perpendiculares a los sucesivos frentes de onda. Estas líneas se denominan rayos y corresponden a las líneas de propagación de la onda. La relación entre rayos y frente de ondas es similar a la de líneas de fuerza y superficies equipotenciales. El tiempo que separa puntos correspondientes de dos superficies de onda es el mismo para todos los pares de puntos correspondientes (teorema de Malus).
Huygens visualizó un método para pasar de un frente de onda a otro. Cuando el movimiento ondulatorio alcanza los puntos que componen un frente de onda, cada partícula del frente se convierte en una fuente secundaria de ondas, que emite ondas secundarias (indicadas por semicircunferencias) que alcanzan la próxima capa de partículas del medio. Entonces estas partículas se ponen en movimiento, formando el subsiguiente frente de onda con la envolvente de estas semicircunferencias. El proceso se repite, resultando la propagación de la onda a través del medio. Esta representación de la propagación es muy razonable cuando la onda resulta de las vibraciones mecánicas de las partículas del medio, es decir una onda elástica pero no tendría significado físico en las ondas electromagnéticas donde no hay partículas que vibren.

![]() A
partir
del
principio
de
Huygens
puede
demostrarse
la
ley
de
la
refracción.
Supongamos
que
un
frente
de
onda
avanza
hacia
la
superficie
refractante
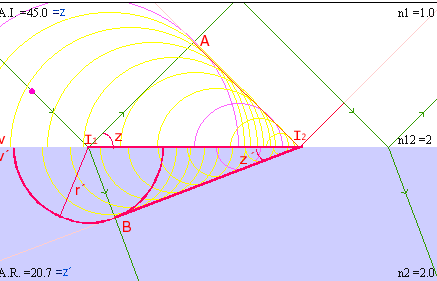
I1I2
que
separa
dos
medios
en
los
cuales
las
velocidades
de
la
luz
son
v
y
v´.
Si
consideramos
I1
como
emisor,
en
el
tiempo Dt
en
que
la
perturbación
llega
de
A
a
I2,
la
perturbación
originada
en
I1
habrá
alcanzado
la
esfera
de
radio r´=
v´Dt.
En
el
mismo
tiempo
la
perturbación
correspondiente
llega
a
todos
los
puntos
de
la
envolvente
BI2,
y
tomando
los
rayos
normales
a
los
frentes
de
onda,
de
la
figura
se
deduce
que:
A
partir
del
principio
de
Huygens
puede
demostrarse
la
ley
de
la
refracción.
Supongamos
que
un
frente
de
onda
avanza
hacia
la
superficie
refractante
I1I2
que
separa
dos
medios
en
los
cuales
las
velocidades
de
la
luz
son
v
y
v´.
Si
consideramos
I1
como
emisor,
en
el
tiempo Dt
en
que
la
perturbación
llega
de
A
a
I2,
la
perturbación
originada
en
I1
habrá
alcanzado
la
esfera
de
radio r´=
v´Dt.
En
el
mismo
tiempo
la
perturbación
correspondiente
llega
a
todos
los
puntos
de
la
envolvente
BI2,
y
tomando
los
rayos
normales
a
los
frentes
de
onda,
de
la
figura
se
deduce
que:
|
|
Þ |
n1 sen ai |
= |
n2 sen ar |
Lo cual está de acuerdo a la experiencia, no sólo en cuanto a direcciones de propagación, sino también en que en el medio de mayor índice de refracción la velocidad es menor, contrariamente a lo que suponían Descartes y Newton.
La
teoría ondulatoria
no
pudo progresar
en
aquella
época
debido
a
la
gran
autoridad
de
Newton
que
la
combatía
arguyendo
que
dicha
teoría
no
podía
explicar
la
propagación
rectilínea.
Otrasinteresantes en Internet con applets.
Escribe tu opinión del artículo en el foro
Revista Digital Sociedad de la información