Un bello problema de Física. Perspectiva histórica.
Plantearse cualquier reto intelectual, sea de cualquier índole, es un asunto inherente al ser humano medianamente civilizado. ¿Acaso no despertó la curiosidad de Tarzán los libros y aprendió sólo a leer y escribir, descifrando las reglas de la gramática, sin saber pronunciar una palabra, únicamente como desafío mental que le diferenciaba del mono?. Esforzarse en resolver un pasatiempos, un estudio de ajedrez, un problema de física, enciende áreas vecinas del cerebro y parecidos esquemas mentales, con mayor o menor complejidad. El ajedrez y la física albergan ciertos paralelismos. Ambas disciplinas se rigen por unas normas o leyes. Parece suficiente pues, conocerlas a fondo para intentar descifrar el juego, pero los enigmas que encierran ciertas situaciones son tan endiablados que no basta con saberse las reglas sino que hay que estar bien familiarizado y poseer buenas dosis de imaginación para que los análisis arranquen.
Para
solucionar un problema primero hay que reconocerlo o inventarlo. En la naturaleza esas
cuestiones están ahí. “Conocidos” los principios que la gobiernan, abordar
y resolver un estudio llega a ser tan placentero como acertar y dar con la clave
para ganar o forzar tablas en aparente desventaja vistas las piezas distribuidas
en un tablero. Trazar un plan, descubrir sutilezas y matices, eliminar
dificultades forma parte del juego. La satisfacción final es la misma que
solventar un damero maldito.
De
esta guisa surgió este bello problema:
Supongamos
que se une por medio de un alambre deformable un punto A a otro B a menor altura
¿qué trayectoria (recta o sinuosa), qué forma debe adoptar el alambre para
que el descenso de una partícula sobre este sea lo más rápido posible?
Galileo
creía que una cuentecilla caería en menor tiempo si el alambre se curvaba. Más
tarde en 1696, Johann Bernoulli intentó averiguar (y lo consiguió de manera
genial) qué clase de curvatura proporciona el descenso más vertiginoso. Esta
curva se conoce como braquistocrona (del griego brachistos, el más breve, y
cronos, tiempo).
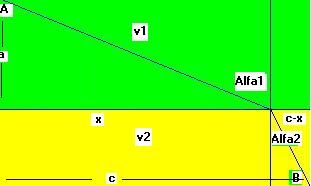
Es posible resolver este hermoso problema desde distintas perspectivas. Históricamente la cuestión entronca con un problema de óptica aparentemente sin relación, la refracción de la luz cuando un rayo cambia de medio en su propagación. Al traspasar la luz a un medio más denso, en el cual la onda se ralentiza, el rayo se desvía. El tiempo requerido para recorrer el camino que parte del punto A y arriba en otro B será:

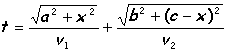
Si
el rayo elige una trayectoria para tardar lo mínimo entonces dt/dx= 0
![]()
|
o bien: |
(ley de la refracción de Snell) |
La
suposición de que la luz va de un punto a otro siguiendo la trayectoria más rápida
se conoce como principio de Fermat (el de la
nota al margen) y proporciona una base sólida para la ley de
Snell.
http://www.phy.ntnu.edu.tw/%7Ehwang/refraction/refraction
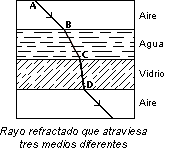
Si en vez de dos medios, la luz atraviesa un camino estratificado en donde en cada capa la velocidad de la luz es v, y disponemos que estas capas sean cada vez más delgadas hasta llegar al límite entonces:
![]()
Esta
situación ocurre aproximadamente cuando un rayo de luz va penetrando en la atmósfera
de densidad creciente.
Al igual que el rayo, la bolita que desciende por el alambre elige el camino más rápido sabiendo que la velocidad que alcanza a una altura no depende del camino seguido (las reglas del juego), solo influye su perdida de energía potencial no la ruta que lo condujo y vale:
|
|
|
suponiendo
que la altura inicial vale 2R y ya veremos por qué.
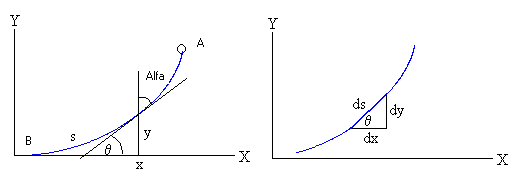
Por trigonometría elemental:
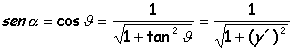
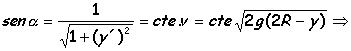
![]()
Que es la ecuación diferencial de una cicloide con el origen en pR,-2R e invertida y cuyas ecuaciones paramétricas se comprueba que son:
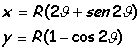
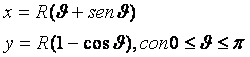
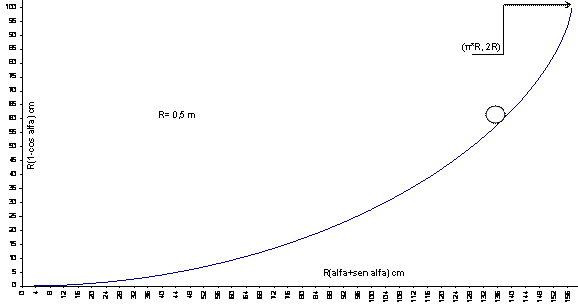
La cicloide es la curva que describe un punto de una circunferencia que rueda sobre una recta sin deslizar como se ve en la figura :

Para
averiguar cuál es el tiempo (mínimo) que tarda la bolita en alcanzar el final
ubicado en el origen partiendo desde una altura 2R a una distancia x=pR
se procede integrando el tiempo:
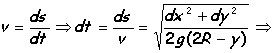
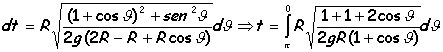
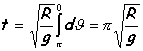
Supongamos que la partícula es una pequeña esfera que rueda sin deslizar, entonces la velocidad será:
Mg2R= ½ mv2+½Iw2+ mgy
Mg2R = ½ mv2+½2/5 mr2v2/r2+ mgy

Es también realmente sorprendente lo que en el año 1673, Christian Huygens (La Haya, 1629-1695), matemático, físico y astrónomo, descubrió, un hecho que le pareció extraordinario en la Cicloide: si un punto se desplaza a lo largo esta curva invertida cuyas ecuaciones están descritas en forma paramétrica, en caída libre, llegará al punto mínimo de la Cicloide en un tiempo que no depende del origen desde donde comenzó a caer. Esta propiedad se la denomina tautócrona (del griego tauto, el mismo).
En la demostración
iniciaremos el descenso a una altura y1 cualesquiera:
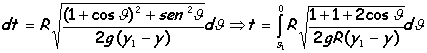
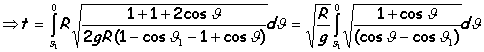
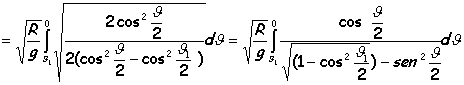
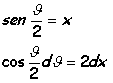
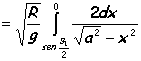
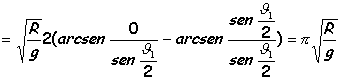
http://www.sc.ehu.es/sbweb/fisica/solido/mov_general/cicloide/cicliode.htm
Huygens fue el primero en descubrir esta propiedad y en darle una aplicación práctica. Estudiando los relojes de péndulo observó que cuando un cronómetro varía la amplitud de la oscilación, entonces deja de contar correctamente. Pero si la lenteja del péndulo se moviese no en una circunferencia, sino a lo largo de una cicloide, entonces aunque la amplitud de oscilación variase, el período permanecería constante.

Para lograr que la lenteja se mueva describiendo una cicloide Huygens se las ingenió mediante una de las propiedades geométricas de la cicloide Si se cuelga el péndulo con una cuerda de longitud 4R y se instala a ambos lados del punto de apoyo una cicloide como extremos, entonces la lenteja describe una cicloide igual. Sea cual sea la amplitud del movimiento oscilatorio el período es el mismo
Jesús Ruiz Felipe. Profesor de Física
Escribe tu opinión del artículo en el foro