
DETERMINACIÓN DE LA CONSTANTE ELÁSTICA
DE UN MUELLE
1.
Método Estático
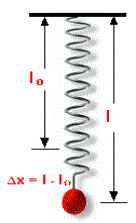
Podemos determinar la constante de un muelle
suspendiendo en él diferentes masas, midiendo los alargamientos que se producen
en cada caso y aplicando la ley de Hooke:
F=- K· Dx
Al colocar una masa el muelle se estira y, después
de una ligera oscilación, se para.
En estas condiciones estáticas se realiza la medida
del alargamiento: a la longitud del muelle estirado (l)se le resta la longitud
inicial ( lo), medidas desde el punto de amarre del muelle hasta el extremo del
muelle)

Se mide la longitud inicial del muelle, lo.
Se colocan distintas masas conocidas (por ejemplo de
10g y luego de 20 en 20 g..) y se mide en cada caso la longitud del muelle
estirado.
Se calcula el peso de cada masa, (mg). Debemos tener
en cuenta el peso portapesas
Se calcula en cada caso: Dx=l
– lo. Se halla K en cada caso.
Tratamiento gráfico:
Supongamos que los alargamientos en un muelle al
colocar distintas masas son las siguientes:
|
Representamos los datos en una gráfica con la
Fuerza peso en ordenadas y los alargamientos, Dx, en
el eje x.
Teóricamente los puntos que resultan deberían
estar sobre una recta de pendiente k según predice la ley de Hooke, pero los
errores experimentales hace que queden fuera de ella. Debemos hallar una recta
cuyos puntos se separen lo menos posible de todos los hallados, que quede lo más
equidistante posible a todos ellos. Una vez hallada la recta se eligen dos
puntos bastante separados para hallar su pendiente. No deben coincidir con los
hallados experimentalmente para que sean puntos de la recta que más se ajusta a
todos.
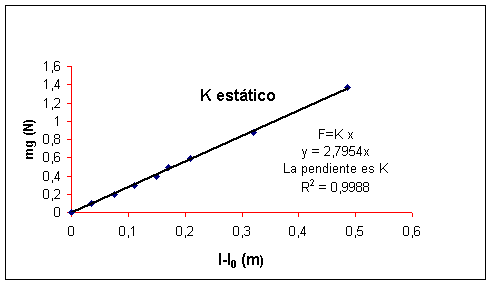
Pendiente =DF / Dx=K
La pendiente de esa recta es m, y en este caso la
constante del muelle, k=2,8 N/m. En la representación se debe observar si algún
valor obtenido se desvía de la media. Si el valor que se aleja está hacia el límite
del alargamiento, puede ser debido a que has sobrepasado el límite de
elasticidad del muelle. En este caso se debe despreciar este valor.
En la determinación de la constante elástica de un
muelle por el método dinámico, lo que hacemos es dejar oscilar el muelle y
medir el período de oscilación.
Si colgamos distintas masa de un muelle y tiramos de
ellas separándolas de su posición de equilibrio, al soltarlas oscilan.
Medimos períodos del muelle para distintas masas
oscilantes (debes tener en cuenta la masa del portapesas).
A partir de la relación de la masa y el período de
oscilación podemos hallar la constante del muelle. Cuelga del muelle diferentes
masas conocidas.
Para cada una de ellas realiza la experiencia
lanzando el muelle y midiendo el tiempo de 20 oscilaciones completas (desprecia
las dos o tres primeras).
Halla el período de una oscilación y registra los
datos en una tabla. Determina en cada caso el valor de k :
K=4 p
2 m / T 2
Determina el valor medio de la constante k (media aritmética).
Tratamiento gráfico:
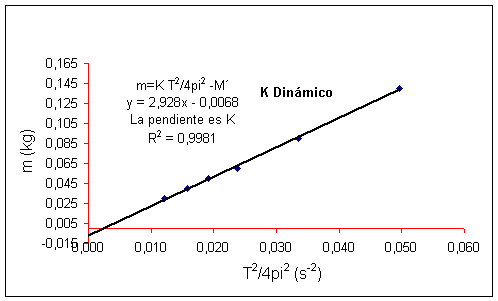
Partiendo de los datos anteriores representamos m en
ordenadas frente a T2/4p2
en
abscisas. Los puntos obtenidos no caen exactamente sobre una recta, pero se
traza una que se aproxime al máximo a todos, haciendo que la distancia de todos
ellos respecto a la recta sea la mínima posible. La pendiente de la recta es la
K del muelle.
Para un mismo muelle los valores de la
constante hallada por los métodos dinámico y estático son ligeramente
diferentes
Al
hallar la constante k de un muelle por el método dinámico se observa que la gráfica
no pasa por el origen. Esto es debido a que no se
considera como oscilante la masa del propio muelle, que también oscila, y en la
fórmula sólo se considera la masa que se cuelga.
Supongamos que la masa del muelle es M.
La parte superior y la inferior del muelle no
oscilan con la misma amplitud , por ello solo una parte de la masa del muelle va
a influir en la masa total oscilante. La masa del muelle se multiplicará por un
factor "f " menor de uno y se sumará a la masa externa.
La masa efectiva del muelle para la oscilación será:
f·M =M´y habrá que sumarla a la masa m:
K=
(m+M´).w2
((m + f·M) 4p2/
T2)=K
m=k T2/4p2
- f·M
Esta ecuación es la de una recta, T2 /4p2
es la
variable independiente y m, la dependiente .
La pendiente de la recta será k
Representando la masa frente al periodo elevado al
cuadrado, para el valor T=0 la recta no pasará por el origen. La ordenada en el
origen será fM=M´. Una vez
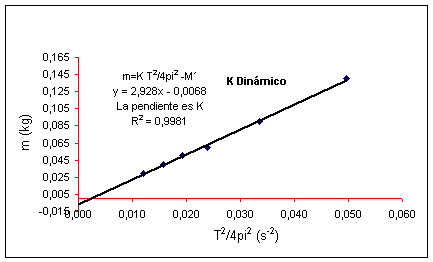
hallada en la gráfica pesamos el muelle y hallamos
"f ". Un valor normal de "f" suele ser entre f=1/3 y f=1/2.
En nuestro caso la masa del muelle es de 15,6 g lo que equivale a una f de 0,43.