Energía en el Movimiento Armónico Simple

La energía cinética de una partícula es Ec = 1/2 mv² = 1/2 mw²A²cos²(wt +f₀), o en función del desplazamiento 

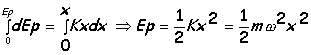
E_c = 1/2 mw²(A²- x²)

Energía potencial

Recordando que F = -dEp/dx y que F = -Kx se obtiene que dEp/dx = Kx

Integrando y eligiendo el cero de la energía potencial en la posición de equilibrio (x=0):

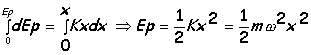
La energía potencial es mínima en la posición de equilibrio y máxima en los extremos x=±A

Sumando la energía cinética y potencial se obtiene la siguiente expresión:

E =Ec +Ep = 1/2 mw²(A²- x²) + 1/2 mw² x² = 1/2 mw²A² = 1/2Kx²

Durante la oscilación, como muestra el diagrama, hay un intercambio de energía cinética y potencial, manteniéndose la energía total constante ya que se trata de una fuerza conservativa. La figura muestra una energía total de 15 unidades correspondientes a la línea horizontal negra. La línea vertical roja muestra la diferencia entre la energía total y la potencial (indicada por la línea discontinua sobre el eje de abcisas) y por tanto corresponde a la energía cinética. Los límites de oscilación están determinados por sus intersecciones con la curva de energía potencial y corresponden a los puntos ±A. En la dirección http://www.sc.ehu.es/sbweb/fisica/default.htm  podemos dar valores a la energía.

Curvas de energía potencial

Representación de la curva de la energía potencial de una partícula de masa m unida a un muelle elástico de constante k, E_p=kx²/2.

    Esta función representa una parábola cuyo vértice está en el origen, que tiene un mínimo en x=0 cuyo valor es E_p=0.

    Las región donde se puede mover la partícula está determinada por la condición de que la energía cinética ha de ser mayor o igual a cero E_k>=0. O bien, que la energía total sea mayor o igual que la energía potencial E>=E_p. Si la partícula tiene una energía total E, la partícula solamente se podrá mover en la región comprendida entre -A y +A, siendo A la amplitud de su M.A.S.

    La intensidad y el sentido de la fuerza viene dado por la pendiente de la recta tangente cambiada de signo. Por tanto, la fuerza que actúa sobre la partícula es negativa a la derecha del origen y positiva a la izquierda.

    En el origen la pendiente es nula, la fuerza es nula, una situación de equilibrio, que por coincidir con un mínimo de la energía potencial es de carácter estable.

    Durante la oscilación hay un intercambio de energía cinética y potencial, manteniéndose la energía total constante ya que se trata de una fuerza conservativa