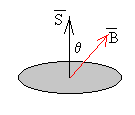
|
|
Se denomina flujo al producto escalar del vector campo por el vector superficie
|
Si el campo no es constante o la superficie no es plana, el flujo se calcula mediante la integral
La inducción electromagnética fue descubierta casi simultáneamente y de forma independiente por Michael Faraday y Joseph Henry en 1830. La inducción electromagnética es el principio sobre el que se basa el funcionamiento del generador eléctrico, el transformador y muchos otros dispositivos.
Supongamos que se coloca un conductor eléctrico en forma de circuito en una región en la que hay un campo magnético. Si el flujo F a través del circuito varía con el tiempo, se puede observar una corriente en el circuito (mientras el flujo está variando). Midiendo la fem inducida se encuentra que depende de la rapidez de variación del flujo del campo magnético con el tiempo.
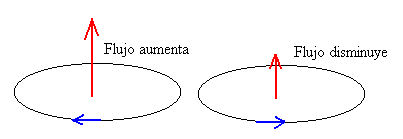
El significado del signo menos, es decir, el sentido de la corriente inducida (ley de Lenz) se muestra en la figura mediante una flecha de color azul..
El campo magnético cuya dirección es perpendicular al plano de la espira, varía con el tiempo de la forma
B=B0 sen(w t)
|
|
El flujo F del campo magnético a través de las N espiras iguales es, el producto del flujo a través de una espira por el número N de espiras
|
La fem inducida en las espiras es
El sentido de la corriente inducida es tal que se opone a la variación de flujo.Se comprueba en:
http://www.walter-fendt.de/ph11s/generator_s.htm
Actividad:
Una
espira cuadrada de alambre está cerca de un cable recto, indefinido, recorrido
por una corriente I como indica la figura.
Explica
razonadamente, en qué sentido circulará la corriente inducida en la espira
|
|
 |
a)
Si aumenta la corriente I.
b)
Si, dejando constante la corriente I, se desplaza la espira hacia la derecha,
manteniéndose en el mismo plano.
http://www.cco.caltech.edu/~phys1/java/phys1/Inductance/Inductance.html
I