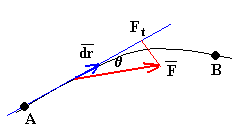

Se denomina trabajo infinitesimal al producto escalar del vector fuerza por el vector desplazamiento.

![]()
Donde Ft es la componente de la fuerza a lo largo del desplazamiento, ds es el módulo del vector desplazamiento, y q el ángulo que forma el vector fuerza con el vector desplazamiento.
El trabajo total a lo largo de la trayectoria entre los puntos A y B es la suma de todos los trabajos infinitesimales
![]()
Cuando la fuerza es constante el trabajo se obtiene multiplicando la componente de la fuerza a lo largo del desplazamiento por el desplazamiento.
W=Ft s
Concepto de energía cinética. Teorema de la Energía Cinética (o de las Fuerzas vivas)
Supongamos que F es la resultante de las fuerzas que actúan sobre una partícula de masa m. El trabajo de dicha fuerza es igual a la diferencia entre el valor final y el valor inicial de la energía cinética de la partícula.
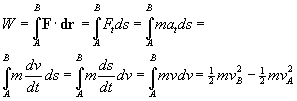
En la primera línea hemos aplicado la segunda ley de Newton; la componente tangencial de la fuerza es igual a la masa por la aceleración tangencial.
En la segunda línea, la aceleración tangencial at es igual a la derivada del módulo de la velocidad, y el cociente entre el desplazamiento ds y el tiempo dt que tarda en desplazarse es igual a la velocidad v del móvil.
Se define energía cinética como la expresión
![]()
El teorema del trabajo-energía indica que el trabajo de la resultante de todas las fuerzas que actúan sobre una partícula es la variación de su energía cinética.
Un fuerza es conservativa cuando el trabajo de dicha fuerza es igual a la diferencia entre los valores inicial y final de una función que solo depende de las coordenadas. A dicha función se le denomina energía potencial.
![]()
El trabajo de una fuerza conservativa no depende del camino seguido para ir del punto A al punto B.
El trabajo de una fuerza conservativa a lo largo de un camino cerrado es cero.
![]()
Ejemplos:
Calculemos el trabajo de la fuerza peso F=-mg j cuando el cuerpo se desplaza desde la posición A cuya ordenada es yA hasta la posición B cuya ordenada es yB.
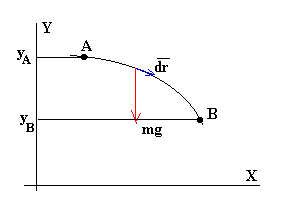
La energía potencial Ep correspondiente a la fuerza conservativa peso tiene la forma funcional
![]()
Donde c es una constante aditiva que nos permite establecer el nivel cero de la energía potencial.
Como vemos en la figura cuando un muelle se deforma x, ejerce una fuerza sobre la partícula proporcional a la deformación x y de signo contraria a esta.
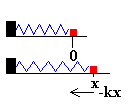 |
F=-kx
El trabajo de esta fuerza es
|
La función energía potencial correspondiente a la fuerza conservativa F vale
![]()
El nivel cero de energía potencial se establece del siguiente modo: cuando la deformación es cero x=0, el valor de la energía potencial se toma cero, Ep=0, de modo que la constante aditiva vale c=0.
![]()
Cuando una partícula está bajo la acción de una fuerza conservativa, el trabajo de dicha fuerza es igual a la diferencia entre el valor inicial y final de la energía potencial
![]()
El trabajo de la fuerza es igual a la diferencia entre el valor final e inicial de la energía cinética.
![]()
Igualando ambos trabajos, obtenemos la expresión del principio de conservación de la energía
EkA+EpA=EkB+EpB
La energía mecánica de la partícula (suma de la energía potencial más cinética) es constante en todos los puntos de su trayectoria.
Para darnos cuenta del significado de una fuerza no conservativa, vamos a compararla con la fuerza conservativa peso.
Cuando la partícula se mueve de A hacia B, o de B hacia A la fuerza de rozamiento es opuesta al movimiento, el trabajo es negativo por que la fuerza es de signo contrario al desplazamiento
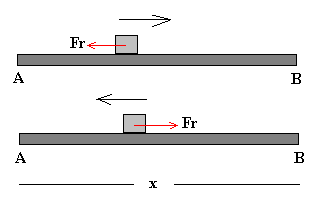 |
WAB=-Fr
x
WBA=-Fr x El trabajo total a lo largo del camino cerrado A-B-A, WABA es distinto de cero WABA=-2Fr x |
En general, sobre una partícula actúan fuerzas conservativas Fc y no conservativas Fnc. El trabajo de la resultante de las fuerzas que actúan sobre la partícula es igual a la diferencia entre la energía cinética final menos la inicial.
![]() (Ek = Energía
cinética)
(Ek = Energía
cinética)
El trabajo de las fuerzas conservativas es igual a la diferencia entre la energía potencial inicial y la final
![]()
Aplicando la propiedad distributiva del producto escalar obtenemos que
| =Wfnc |
El trabajo de una fuerza no conservativa es igual a la variación de la energía mecánica (cinética más potencial) de la partícula.