
APLICACIÓN A SATÉLITES
Para simplificar los cálculos suponemos que el satélite se mueve con trayectoria circular, siendo r el radio de la órbita (la distancia del centro de la tierra al satélite).
Fc = Fg
Conociendo el radio de rotación, se calcula el periodo de la órbita: Actividad. Calcular el periodo de rotación de la estación internacional sabiendo que orbita a unos 400 Km de altura.
Los satélites geoestacionarios tienen un periodo de 24 horas, de tal manera que siempre se encuentran sobre el mismo punto de la tierra. El radio de su órbita es de unos 36.000 Km
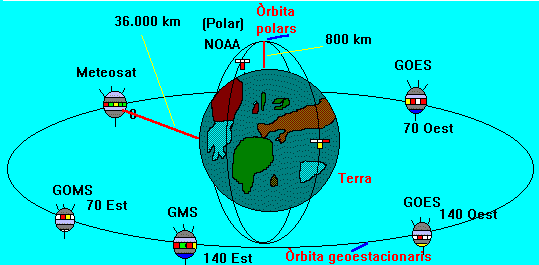
Conociendo uno de estos 3 datos (radio de la órbita, velocidad o periodo) implícitamente conocemos los otros 2:
Comprueba que esto es cierto en http://surendranath.tripod.com/Kepler/Kepler.html
Energía:
El hecho de que la fuerza de atracción sea conservativa, implica que la energía total (cinética más potencial) de la partícula es constante, en cualquier punto de la trayectoria.
![]()
Calcularemos ahora la energía que debe tener un satélite para mantenerse en una órbita circular estacionaria a una altura h sobre la superficie de la Tierra.
Cuando está en órbita, se debe cumplir que los valores de la fuerza centrípeta y de la fuerza de atracción gravitatoria coincidan.
![]()
de donde :
![]()
y su energía cinética:
![]()
Por otra parte, la energía potencial es:
![]()
y la energía total, llamada energía de enlace es:
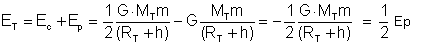 |
< 0 |
la energía de un satélite en órbita es siempre negativa y coincide con la mitad de su energía potencial. Para enviar un objeto fuera del campo gravitatorio terrestre la energía debe ser igual o superior a cero
Conocida la energía potencial gravitatoria, se puede calcular la velocidad que debe adquirir un cuerpo de masa m para que escape de la atracción de la Tierra.
Si el cuerpo esta inicialmente en reposo, su velocidad debe aumentar hasta un valor ve, tal que la energía cinética que adquiera sea igual, en el momento de escape, a la energía potencial:
![]()
Con lo que la velocidad de escape es:
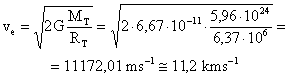
Que sólo depende de la masa de la Tierra y no de la masa del cuerpo. El mismo razonamiento se podría aplicar a cualquier otro planeta.
Da un valor negativo a la energía en: http://www3.adnc.com/%7Etopquark/fun/JAVA/Kepler/Kepler2.html
La energía de una órbita es siempre negativa. Para enviar un objeto fuera del campo gravitatorio terrestre la energía debe ser igual o superior a cero