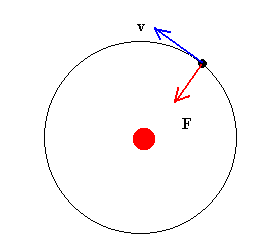
Combinando estas expresiones, obtenemos
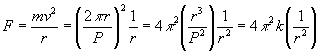
Vemos que la fuerza F que actúa sobre el planeta en órbita circular es inversamente proporcional al cuadrado de la distancia r desde el centro de fuerzas al centro del planeta.

Teoría
de la gravitación universal.
La naturaleza cuadrático inversa de la fuerza centrípetra para el caso de órbitas circulares, puede deducirse fácilmente de la tercera ley de Kepler sobre el movimiento planetario y de la dinámica del movimiento circular uniforme:
Según la tercera ley de Kepler el cuadrado del periodo es proporcional al cubo del semieje mayor de la elipse, que en el caso de la circunferencia es su propio radio, P2=kr3.
La dinámica del movimiento circular uniforme, nos dice que en una trayectoria circular la fuerza es igual al producto de la masa por la aceleración normal, F= mv2/r.
El tiempo que tarda un planeta en dar una vuelta completa es el cociente entre la longitud de la circunferencia y la velocidad, P=2p r/v.
|
|
Combinando estas expresiones, obtenemos
Vemos que la fuerza F que actúa sobre el planeta en órbita circular es inversamente proporcional al cuadrado de la distancia r desde el centro de fuerzas al centro del planeta. |
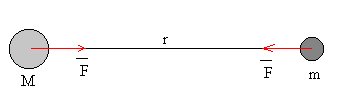
La interacción entre dos cuerpos de masa M y m se describe en término de una fuerza atractiva, cuya dirección es la recta que pasa por el centro de los dos cuerpos y cuyo módulo viene dado por la expresión
![]()
G es la constante de la gravitación universal G=6.67·10-11 Nm2/kg2, y r es la distancia entre los centros de los cuerpos.
Comprobación de la Ley:
Newton comparó la aceleración centrípeta de la Luna con la aceleración de la gravedad g=9.8 m/s2. La aceleración centrípeta de la Luna es ac=v2/r=4p 2r/P2, con r=3.84 108 m y P=28 días=2.36 106 s, se obtiene ac=2.72 10-3 m/s2. Por consiguiente,
![]()
Como el radio de la Tierra es 6.37 106 m, y el radio de la órbita de la Luna es 3.84 108 m, tenemos que
![]()
Por tanto,
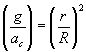
Las aceleraciones de ambos cuerpos están en razón inversa del cuadrado de las distancias medidas desde el centro de la Tierra.
En la física anterior a Newton una manzana cae verticalmente hacia la Tierra en una trayectoria rectilínea, mientras que la Luna describe una órbita casi circular, que es una trayectoria cerrada. ¿Cómo estas dos categorías de movimientos pueden estar relacionados?
Si la manzana que caía verticalmente es empujado por la fuerza del aire, su trayectoria ya no será rectilínea sino el arco de una curva. Por ejemplo un proyectil disparado desde un cañón describe una trayectoria parabólica tal como se observaba en el siglo XVII en el que vivió Newton . El salto conceptual que llevó a cabo Newton fue el de imaginar que los proyectiles podrían ser disparados desde lo alto de una montaña describiendo trayectorias elípticas (siendo la parábola una aproximación de la elipse).
Por tanto, la manzana y la Luna están cayendo, la diferencia es que la Luna tiene un movimiento de caída permanente, mientras que la manzana choca con la superficie de la Tierra.
Una misma causa produce, por tanto, los movimientos de los cuerpos celestes y terrestres.
"Si consideramos los movimientos de los proyectiles podremos entender fácilmente que los planetas pueden ser retenidos en ciertas órbitas mediante fuerzas centrípetras; pues una piedra proyectada se va apartando de su senda rectilínea por la presión de su propio peso y obligada a describir en el aire una curva, cuando en virtud de la sola proyección inicial habría debido continuar dicha senda recta, en vez de ser finalmente atraída al suelo; y cuanto mayor es la velocidad con la cual resulta ser proyectada más lejos llega, antes de caer a tierra. Podemos por eso suponer que la velocidad se incremente hasta que la piedra describa un arco de 1, 2, 5, 10, 100, 1000 millas antes de caer, de forma que al final, superando los límites de la Tierra, pasará al espacio sin tocarla..."
En la figura, se representa las curvas que un cuerpo describiría si fuese proyectado en dirección horizontal desde la cima de una alta montaña a más y más velocidad.
Abrir la página :http://www.phys.virginia.edu/classes/109N/more_stuff/Applets/newt/newtmtn.html y averiguar a qué velocidad se deberá lanzar un proyectil en las proximidades de la tierra para que describa una vuelta entera (se ponga en órbita).
Entonces, por la misma razón que un cuerpo proyectado con menos velocidad describe el arco menor y, proyectado con más velocidad, un arco mayor, al aumentar la velocidad, terminará por llegar bastante más allá de la circunferencia de la Tierra, retornando a la montaña desde la que fue lanzada.